- Airtable Community
- Discussions
- Ask A Question
- Formulas
- Mod formula assistance
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Mod formula assistance
- Mark as New
- Bookmark
- Subscribe
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
May 14, 2020 02:47 AM
I am trying to understand a why a simple MOD function isn’t returning the correct answer.

Airtable: Organize anything you can imagine
Airtable works like a spreadsheet but gives you the power of a database to organize anything. Sign up for free.
( I can grant you access so you can see the formulas)
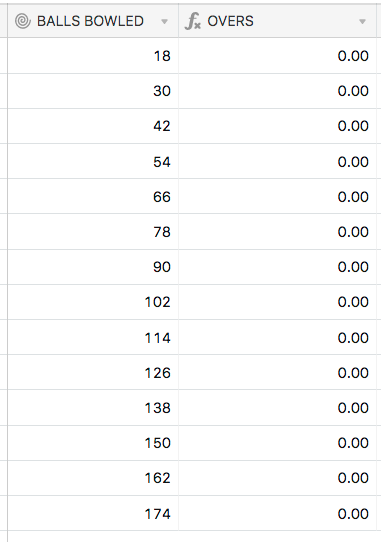
On the table titled “SEASON STATS OVERVIEW”, in the OVER field, I am trying to build a larger formula and part of it requires me to use the MOD function. The formula in the OVERS field is MOD({BALLS BOWLED},6) but for some reason the record for player 2 is returning a value of 6 when it should be 0. I have tested the MOD function for the number 30 as a number i.e. not generated from a roll up function and that works. But for some reason when the number 30 is generated from a Roll up formula is returns an incorrect value.
I can grant creator access to you if you need to see the formula fields/
Any ideas/assistance, all gratefully received.
Thanks in advance
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
May 14, 2020 08:22 AM
I copied the base and am playing in that copy, so you can remove my access to your original.
After messing with it a bit, I don’t think it’s a problem with MOD, but rather a side-product of some of the math taking place leading up to that, and how those values are being represented internally, regardless of how they appear based on the field formatting options.
First off, using SUM(values) as your aggregation function should return a number, so forget what I said above about the array-to-string-to-number conversion process. That’s not necessary.
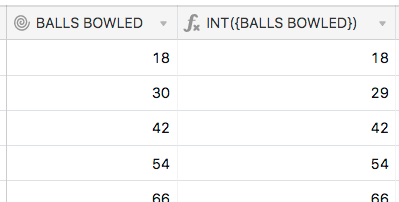
Here’s one of the primary clues that leads me to think that the internal numbers are not as clean as they appear. I made a test formula to force {BALLS BOWLED} to an integer:
INT({BALLS BOWLED})
Putting that next to {BALLS BOWLED}, the result for that problem line surprised me:
Because the INT() function “Returns the greatest integer that is less than or equal to the specified value.”, that tells me that the true value of {BALLS BOWLED} isn’t an even 30 like the field displays, but actually 29.??? However, I wasn’t able to see that detail by forcing {BALLS BOWLED} to display as a decimal, even with the highest precision formatting option.
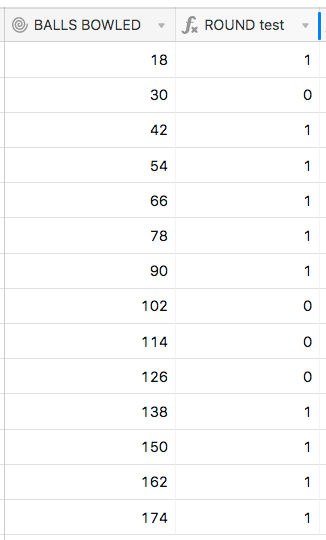
My next test was to try to round the value with the ROUND() function, and see how the rounded value compared to the unrounded one:
ROUND({BALLS BOWLED}, 0) = {BALLS BOWLED}
Based on the earlier INT() test, the results didn’t totally surprise me, but also showed that other values were also not as clean as they appeared on the surface:
In the end, applying ROUND() in your {OVERS} field did the trick:
MOD(ROUND({BALLS BOWLED}, 0), 6)
Why isn’t the value cleaner even though you’re using a combination of rounding functions leading up to that? No idea.
- Mark as New
- Bookmark
- Subscribe
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
May 14, 2020 06:32 AM
Is Balls Bowled a number field? What is the value in Balls Bowled?
- Mark as New
- Bookmark
- Subscribe
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
May 14, 2020 06:54 AM
Hi there, if you click on this link and request access, I’ll grant it to you. You’ll then be able to see all the fields. It might make it easier
- Mark as New
- Bookmark
- Subscribe
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
May 14, 2020 07:22 AM
Unless your Roll-up field’s aggregation formula is designed a certain way, it will return an array, even if that array is only a single value. You have two options: modify the rollup aggregation formula to force the result to a number, or convert the array to a number in your {OVERS} field. Not knowing your aggregation formula, I’ll go with the second option.
It’s actually going to be a two-step process: array to string, then string to number. To go from an array to a string, concatenate the array with an empty string:
{BALLS BOWLED} & ""
To turn that into a number, wrap it inside the VALUE() function:
VALUE({BALLS BOWLED} & "")
Your final formula in {OVERS} then becomes:
MOD(VALUE({BALLS BOWLED} & ""), 6)- Mark as New
- Bookmark
- Subscribe
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
May 14, 2020 07:41 AM
Hi Justin,
Thank you for trying to help me with this. Much appreciated.
Unless I am doing something very wrong, that didn’t seem to work. It might be easier if I grant you access to the base so you can see everything. If you click on this link, I will grant you creator access
- Mark as New
- Bookmark
- Subscribe
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
May 14, 2020 07:49 AM
Access requested. You could also share a copy of the base without needing to grant access. Open the share options, choose “Create a shared link to the whole base,” then choose “Private read-only link”. Others using that link can then make a copy of the base using the “Copy base” option in the upper right corner.
- Mark as New
- Bookmark
- Subscribe
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
May 14, 2020 07:51 AM
Thank you that’s good to know. I wasn’t aware. I have granted someone else access but they haven’t come back to me yet, so you may want to copy the base to avoid and overwriting
- Mark as New
- Bookmark
- Subscribe
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
May 14, 2020 08:22 AM
I copied the base and am playing in that copy, so you can remove my access to your original.
After messing with it a bit, I don’t think it’s a problem with MOD, but rather a side-product of some of the math taking place leading up to that, and how those values are being represented internally, regardless of how they appear based on the field formatting options.
First off, using SUM(values) as your aggregation function should return a number, so forget what I said above about the array-to-string-to-number conversion process. That’s not necessary.
Here’s one of the primary clues that leads me to think that the internal numbers are not as clean as they appear. I made a test formula to force {BALLS BOWLED} to an integer:
INT({BALLS BOWLED})
Putting that next to {BALLS BOWLED}, the result for that problem line surprised me:
Because the INT() function “Returns the greatest integer that is less than or equal to the specified value.”, that tells me that the true value of {BALLS BOWLED} isn’t an even 30 like the field displays, but actually 29.??? However, I wasn’t able to see that detail by forcing {BALLS BOWLED} to display as a decimal, even with the highest precision formatting option.
My next test was to try to round the value with the ROUND() function, and see how the rounded value compared to the unrounded one:
ROUND({BALLS BOWLED}, 0) = {BALLS BOWLED}
Based on the earlier INT() test, the results didn’t totally surprise me, but also showed that other values were also not as clean as they appeared on the surface:
In the end, applying ROUND() in your {OVERS} field did the trick:
MOD(ROUND({BALLS BOWLED}, 0), 6)
Why isn’t the value cleaner even though you’re using a combination of rounding functions leading up to that? No idea.
- Mark as New
- Bookmark
- Subscribe
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
May 14, 2020 08:23 AM
It looks like you will need to round your original value of “Balls Bowled”, because if you look at the new formula that I just created, which is: {BALLS BOWLED} & "", it results in non-integer values.
So this formula will work for you:
MOD(ROUND({BALLS BOWLED},0),6)
- Mark as New
- Bookmark
- Subscribe
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
May 14, 2020 08:24 AM
Oh, LOL, @Justin_Barrett and I both posted the same formula at the exact same time. :slightly_smiling_face: